[Leetcode] 42. Trapping Rain Water

문제 링크 : https://leetcode.com/problems/trapping-rain-water/description/

🖥️ 시작하며

처음 접근이 어려웠던 문제였다.

우선 height 배열에 검은색 블럭의 높이가 주어지고, 비가 왔을 시 웅덩이가 생기는 칸이 몇 칸인지 답을 도출해야 하는 문제다.

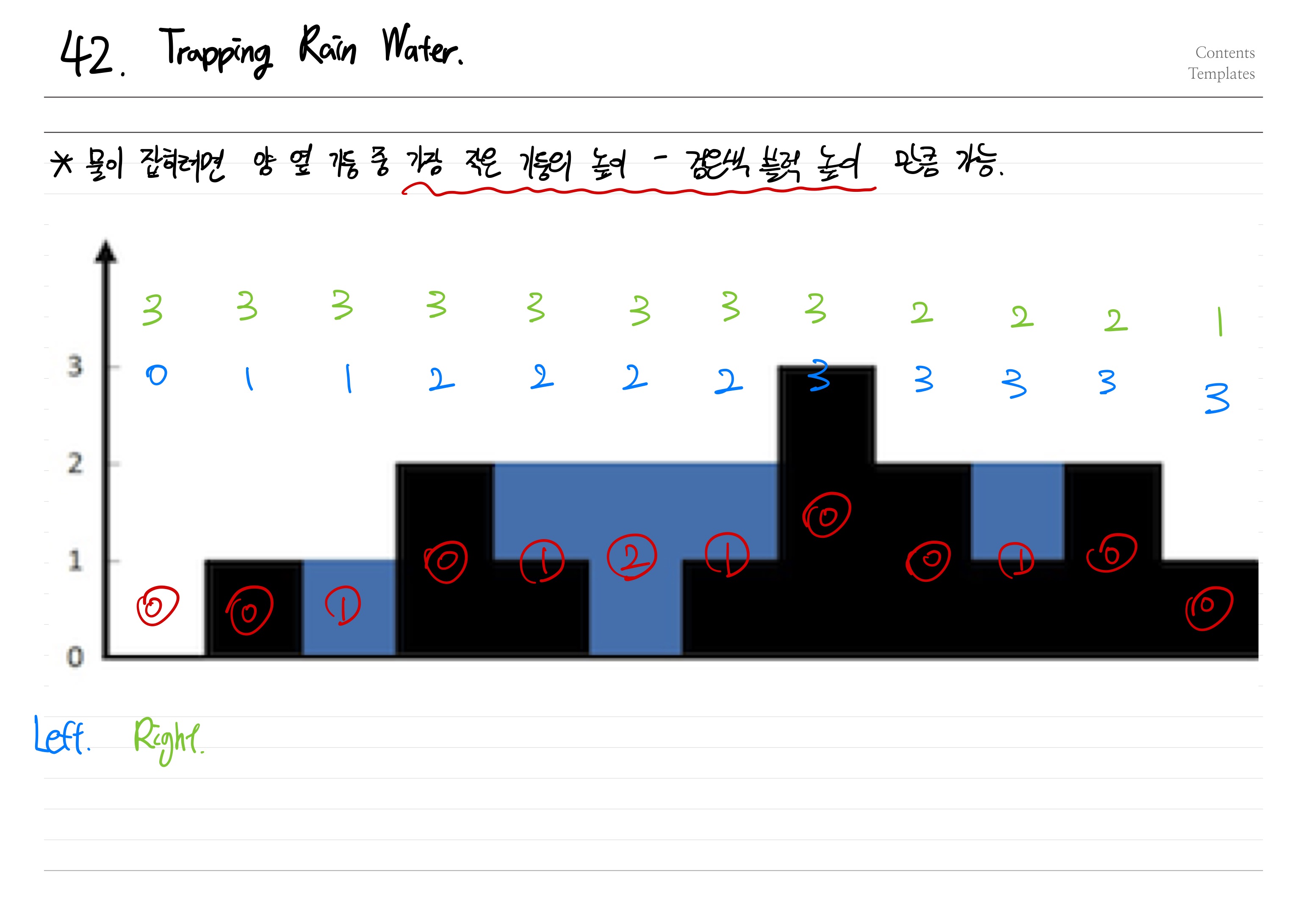
아마 직관적으로는 왼쪽 벽과 오른쪽 벽 중 낮은 벽의 높이로 바로 접근할 수 있지 않나 싶다.

그래서 본인은 왼쪽 벽의 최대 높이를 저장하는 배열, 오른쪽 벽의 최대 높이를 저장하는 배열을 생성하는 쪽으로 가닥을 잡았다.

아래 그림을 중심으로 파헤쳐보자.

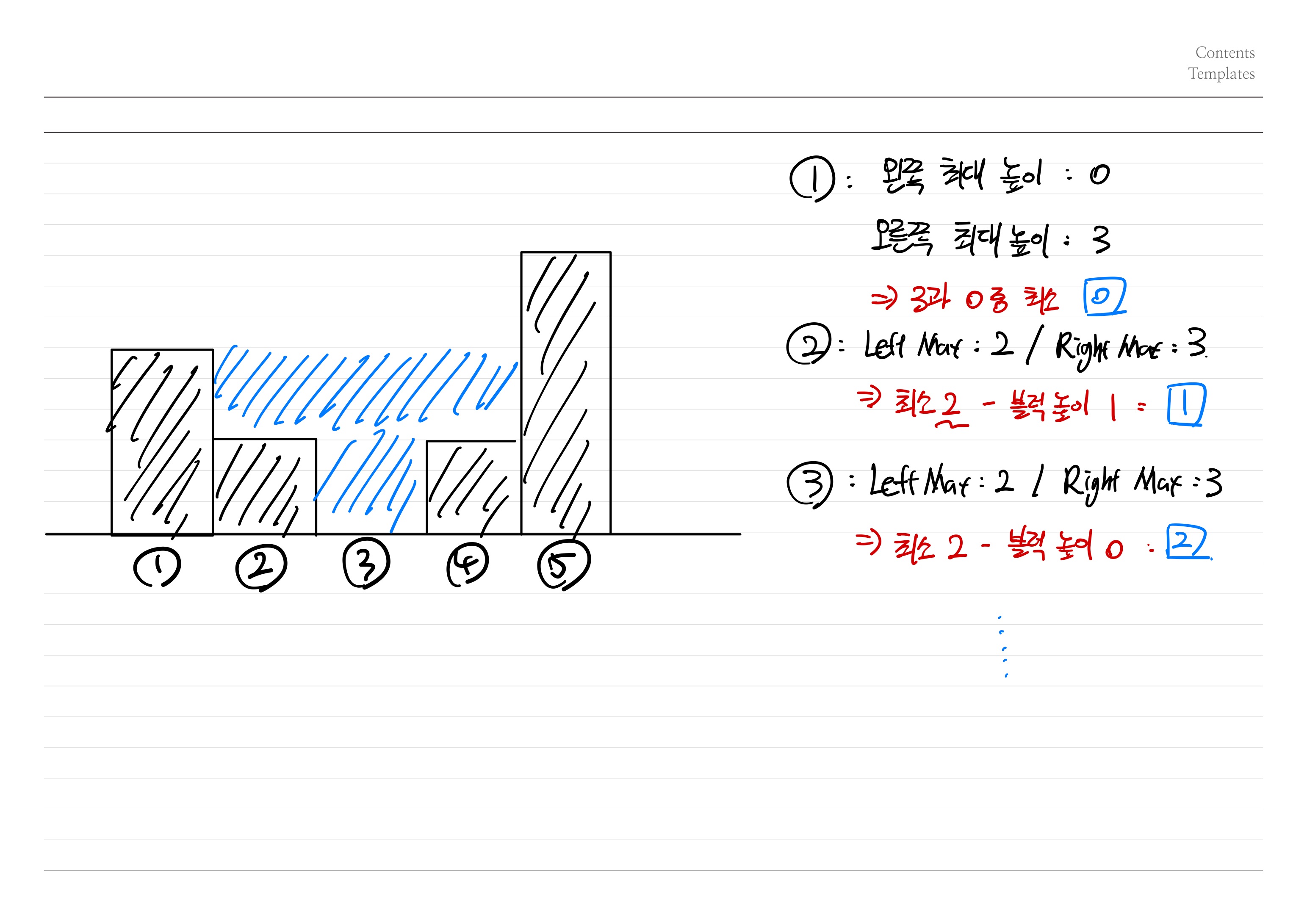
결국 이를 식으로 풀어내자면

**왼쪽과 오른쪽 벽의 최솟값 - 검은색 블록 높이** 라고 할 수 있다.

Python

class Solution:
    def trap(self, height: List[int]) -> int:
        if not height:
            return 0

        res = 0
        H = len(height)

        leftMax = [0] * H
        rightMax = [0] * H

                # 왼쪽 최대 높이 벽 저장
        leftMax[0] = height[0]
        for i in range(1, H):
            leftMax[i] = max(leftMax[i - 1], height[i])

                # 오른쪽 최대 높이 벽 저장
        rightMax[H - 1] = height[H - 1]
        for i in range(H - 2, -1, -1):
            rightMax[i] = max(rightMax[i + 1], height[i])

                # 계산
        for i in range(H):
            res += min(leftMax[i], rightMax[i]) - height[i]

        return res

C++

class Solution {
public:
    int trap(const std::vector<int>& height) {
        if (height.empty()) {
            return 0;
        }

        int H = height.size();
        int res = 0;

        std::vector<int> leftMax(H);
        std::vector<int> rightMax(H);

        // 왼쪽에서부터 최대 높이 저장
        leftMax[0] = height[0];
        for (int i = 1; i < H; ++i) {
            leftMax[i] = std::max(leftMax[i - 1], height[i]);
        }

        // 오른쪽에서부터 최대 높이 저장
        rightMax[H - 1] = height[H - 1];
        for (int i = H - 2; i >= 0; --i) {
            rightMax[i] = std::max(rightMax[i + 1], height[i]);
        }

        // 물을 잡을 수 있는 양 계산
        for (int i = 0; i < H; ++i) {
            res += std::min(leftMax[i], rightMax[i]) - height[i];
        }

        return res;
    }
};

소감

DP나 다른 방식을 떠올리다가 시간이 많이 걸렸다. 알고리즘 다시 준비하는걸로..

부록

참고문헌

---